Ρε μεγάλε, ακόμα δεν πρόλαβες να μπεις στα νερά και έκανες και κατατομή κανόνος!! Προχωρημένο σε βρίσκω... Ο τρόπος που γράφεις ότι κατάλαβες τα πράγματα αντανακλά αν όχι ακριβώς, τουλάχιστον πάνω-κάτω την πραγματικότητα. Οι λόγοι της κλίμακας πράγματι βρέθηκαν με τη λογική του τρόπου που περιγράφεις, ο οποίος εξηγήθηκε πλήρως από τον Ευκλείδη στο έργο του "Κατατομή Κανόνος". Το έχει εκδώσει ο κ. Σπυρίδης. Επίσης, ο τρόπος του Ευκλείδη περιγράφεται πολύ ωραία και στο εξαιρετικό βιβλίο του Μαυροειδή "Οι μουσικοί τρόποι στην Ανατολική Μεσόγειο", το οποίο σου συνιστώ να προμηθευτείς οπωσδήποτε! Εκεί θα βρεις και τις απαντήσεις στις υπόλοιπες απορίες σου.
Μου έδωσες όμως ιδέα να αναφερθώ και στη μαλακή διατονική κλίμακα και όχι μόνο στη σκληρή (αυτό ουσιαστικά θέλεις και είναι λογικό, αφού αυτή η κλίμακα είναι η βασική κλίμακα της βυζαντινής μουσικής). Λοιπόν, το πράγμα έχει ως εξής (συγγνώμη για την προχειρότητα, τα γράφω επιτόπου, μια και δεν τα έχω περιλάβει στη μελέτη μου, θα τα περιλάβω όμως και σ' ευχαριστώ για την επισήμανση):
Μετά τον Πυθαγόρα, που έζησε τον 6ο π.Χ. αι., ακολούθησαν κι άλλοι θεωρητικοί που διατύπωσαν διαστήματα. Η διαφορά ήταν ότι ο Πυθαγόρας ήταν μαθηματικός, αρκέστηκε στους βασικούς λόγους της οκτάβας, της τετάρτης, της πέμπτης και στους εξ αυτών παραγόμενους του τόνου και του λείμματος (και όχι ημιτονίου όπως γράφεις, νομίζω το εξηγήσαμε) και με βάση αυτούς εξέφρασε τα διαστήματα της κλίμακας. Το θέμα όμως είναι ότι
τα ενδιάμεσα του τετραχόρδου διαστήματα (οι κινούμενοι φθόγγοι δηλ.) στη μουσική πράξη δεν ήταν τόσο στάνταρ όσο τους εξέφρασε ο Πυθαγόρας, παρά εκτελούνταν όχι μόνο με τον τρόπο του Πυθαγόρα, αλλά και σε αποστάσεις διάφορες του τόνου (στο διάτονο) ή του τόνου+λείμματος (στο χρώμα). Έτσι όλοι οι υπόλοιποι θεωρητικοί, πολλοί από τους οποίους ήταν όχι μόνο μαθηματικοί, αλλά και μουσικοί, συνειδητοποίησαν αμέσως την ανάγκη να εκφράσουν θεωρητικά και πιο "μαλακά", ας πούμε, διαστήματα. Δεν απέρριψαν ποτέ τα πυθαγόρεια, απλώς είδαν ότι δεν ήταν αρκετά για να εκφράσουν το σύνολο της μουσικής πράξης.
Αποκορύφωμα της τάσης αυτής ήταν ο Αριστόξενος (4ος π.Χ. αι.), ο οποίος ήταν μουσικός και είδε το θέμα καθόλου μαθηματικά αλλά μουσικά και μόνο, εκφράζοντας μάλιστα τα διαστήματα όχι με λόγους, αλλά με αναλογίες του τόνου, ορίζοντας:
- το σκληρό διάτονο σε 1/2, 1/1 και 1/1 του τόνου (6, 12, 12)
- το μαλακό διάτονο σε 1/2, 3/4 και 5/4 του τόνου (6, 9, 15)
Από τότε οι μουσικοί στην αρχαία Ελλάδα χωρίστηκαν σε Πυθαγορείους και Αριστοξενικούς, με τους πρώτους να δίνουν έμφαση στη μαθηματική ακρίβεια και τους δεύτερους στη μουσική πρακτική και να κάνουν λόγο για διαιρέσεις σε τρίτα και τέταρτα του τόνου και διαίρεση του τόνου σε "δωδεκατημόρια" (εξ ου και τα 72 τμήματα της αριστοξένειας κλίμακας, αν ο τόνος είναι 12 και το ημιτόνιο 6).
Στα Ελληνιστικά μεταχριστιανικά χρόνια εμφανίστηκε ο Δίδυμος, ο οποίος έκανε την εξής σκέψη (την αναφέρει και αυτήν πολύ ωραία ο Μαυροειδής): θέλοντας να εκφράσει τα πιο μαλακά διατονικά διαστήματα της μουσικής πράξης, είδε ότι
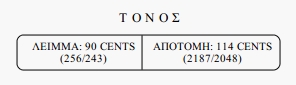
αν αντικαταστήσει στο σκληρό πυθαγόρειο τετράχορδο 9/8 - 9/8 - 256/243 το λείμμα 256/243 (=5.4/72) με την αποτομή 2187/2048 (=6.8/72), που είναι το υπόλοιπο έως τον τόνο διάστημα (υπενθυμίζω ότι ο τόνος 9/8 είναι όχι 12 αλλά 12.2/72) προκύπτει το εξής τετράχορδο:
9/8, 65536/59049, 2187/2048 (12.2 - 10.8 - 6.8)
Αυτό το 65536/59049 είναι, ας πούμε, ο ελάσσων πυθαγόρειος τόνος, που προκύπτει, σε σύγκριση με τον μείζονα, αν του αφαιρέσουμε ένα πυθαγόρειο κόμμα (=διαφορά λείμματος και αποτομής)
Το θέμα όμως ήταν ότι οι αριθμοί αυτοί ήταν πολύ μεγάλοι, προκειμένου να γίνουν αντιληπτοί και να εφαρμοστούν σε όργανο. Έτσι ο Δίδυμος βρήκε τους μικρότερους δυνατούς λόγους που εκφράζουν στο περίπου τους αριθμούς αυτούς και οι οποίοι δεν είναι άλλοι από τους γνωστούς στην επιστήμη της μουσικολογίας:
9/8, 10/9, 16/15 (12.2 - 10.9 - 6.7)
Στην ουσία δηλ. παρήγαγε στον "ελάσσονα" τόνο αφαιρώντας όχι ένα πυθαγόρειο, αλλά ένα διδύμειο κόμμα (=διαφορά 9/8 και 10/9 = 81/80). Το τεράστιο συγγραφικό έργο του Διδύμου έχει χαθεί, όμως μας διασώζει αρκετά στοιχεία απ' αυτό ο Πτολεμαίος (2ος μ.Χ. αι.), ο οποίος και έκανε ευρεία χρήση των επιμορίων λόγων, όπως ξαναείπαμε (αυτών δηλ. με διαφορά ενός αριθμού μεταξύ αριθμητή και παρονομαστή), ο οποίοι ονομάστηκαν έκτοτε και πτολεμαϊκοί.
Αργότερα η φυσική επιστήμη και η επιστήμη της ακουστικής απεφάνθη ότι με τη χρήση των λόγων αυτών τα διαστήματα ακούγονται πολύ σωστά και δεν ευνοούνται τα λεγόμενα διακροτήματα (για περισσότερα ρωτήστε το Δημήτρη τον Ανδριώτη...). Έτσι
η κλίμακα που χρησιμοποιούσε τους λόγους του Διδύμου και διαστήματα 12-11-7 (συγκερασμένα στο ακέραιο στην κλίμακα των 72) ονομάστηκε "φυσική κλίμακα" (ίδιος συγκερασμός φυσικά προκύπτει και στα διαστήματα της μαλακής πυθαγόρειας κλίμακας, με τη χρήση της αποτομής, αφού διαφέρουν ελάχιστα και σε βαθμό που δεν γίνεται αντιληπτός ακουστικά "ούτε με σφαίρες"...). Η κλίμακα αυτή, με μια μικρή τροποποίησή της, χρησιμοποιήθηκε στην ευρωπαϊκή μουσική από τον Zarlino, που την καθιέρωσε τον 16ο αι., μέχρι τον Μπαχ, που εισήγαγε ως συνθέτης στη δυτική μουσική τη σημερινή σκληρή διατονική κλίμακα τον 17ο αι. (μετά τη μαθηματική θεμελίωση από τον Βερκμάιστερ).
Τώρα, πώς προέκυψε η κλίμακα της βυζαντινής μουσικής; Ως εξής: όσο κι αν φαίνεται περίεργο, μέχρι το Χρύσανθο δεν είχαμε στην ουσία ορισμό διαστημάτων βυζαντινής μουσικής, καθώς στις λίγες περιπτώσεις που αυτός έγινε, ήταν αντιγραφή των διαστημάτων του Πτολεμαίου. Υπόψιν ότι όλους αυτούς τους αιώνες, οι λαοί της Ανατολής και κυρίως οι Άραβες έκαναν πολύ δουλειά πάνω στα διαστήματα, ενώ η μουσική μας επηρεάστηκε σαφώς από τη λόγια ανατολική μουσική, με την οποία και ομοιάζει περισσότερο, παρά με την αρχαία ελληνική, από την οποία όμως οι βασικές έννοιες (τετράχορδα, τρόποι κλπ.) μεταλαμπαδεύτηκαν εν τω μεταξύ στην Ανατολή, δεδομένου ότι οι Άραβες ήταν γενικώς εμβριθείς μελετητές των Αρχαίων Ελλήνων.
Μέσα σ' αυτή την πραγματικότητα λοιπόν, στην ενιαία λεκάνη της Ανατολής, που όλοι έπαιζαν την πανδουρίδα, το νέυ και τέτοια πράγματα, έρχεται ο Χρύσανθος και πρώτος δίνει τα διαστήματα της βυζαντινής κλίμακας όχι με λόγους αντιγραμμένους από αρχαίους Έλληνες θεωρητικούς, αλλά προσπαθώντας να εκφράσει τη βυζαντινή μουσική αυτή καθαυτή και όχι την αρχαία, όπως ο Στεφανίδης,
ούτε την ανατολική, όπως ο Κώνστας (σύγχρονοί του θεωρητικοί, εκ των οποίων ο πρώτος εκφράζεται με αρχαιοελληνικές ορολογίες και ο δεύτερος με ορολογίες ανατολικών μακαμιών!)
Οι λόγοι λοιπόν που δίνει ο Χρύσανθος για το μαλακό διατονικό τετράχορδο είναι (Θεωρητικό του 1832):
9/8, 12/11, 88/81 (12.2 - 9 - 8.6), δηλ. με συγκερασμό στο ακέραιο 12-9-9/72. Ίδιοι ακριβώς λόγοι με αυτούς που είχαν δώσει, αρκετούς αιώνες πριν, μεγάλοι άραβες θεωρητικοί και ίδιοι επίσης με αυτούς που γίνονται σήμερα δεκτοί στο διατονικό γένος της αραβικής μουσικής.
Το μεγάλο και πολυσυζητημένο θέμα είναι ότι
ο Χρύσανθος έκανε λάθος στο συγκερασμό και εξέφρασε τους λόγους αυτούς με τμήματα 12-9-7, μεταχειριζόμενος κλίμακα 68 τμημάτων. Έτσι, ενώ με τους λόγους ο ελάσσων και ο ελάχιστος τόνος εμφανίζουν διαφορά ούτε μισού μορίου, με τα τμήματα εμφανίζονται να απέχουν δύο ολόκληρα μόρια! Το ακόμα μεγαλύτερο όμως θέμα κατ' εμέ είναι ότι
οι μεταγενέστεροι του Χρυσάνθου συνέχιζαν να εκφράζονται όχι με τους λόγους του Χρυσάνθου, αλλά με τα τμήματα, η λογική των οποίων επομένως πιστεύω εγώ ότι εξέφραζε την πράξη της μουσικής μας: δηλ.
- ο ελάσσων και ο ελάχιστος τόνος δεν είναι σχεδόν όμοιοι, όπως στους λόγους, αλλά διαφοροποιούνται (9 και 7)
- ο ελάσσων απέχει περισσότερο από το μείζονα απ' ότι ο ελάχιστος από τον ελάσσονα (12-9 σε σύγκριση 9-7)
Είναι ευνόητο ότι δεν μπορούσε να διαιωνίζεται αυτό το λάθος του Χρυσάνθου και η ασυνέπεια μεταξύ λόγων και τμημάτων κλίμακας κι έτσι η Πατριαρχική Επιτροπή ήρθε το 1883 και έκανε τα εξής:
- Άλλαξε την για πολλούς λόγους ελαττωματική κλίμακα του Χρυσάνθου των 68 τμημάτων και εισήγαγε αυτή των 72, που δίνει πολύ σωστότερες αναλογίες κατά το συγκερασμό
- Απεφάνθη ότι τα διαστήματα πρέπει να τα βρούμε όχι βασιζόμενοι σε κάποιες λογικές-μαθηματικές σκέψεις (βασικά τα επίμαχα διαστήματα του ελάσσονος/ελαχίστου τόνου και του χρωματικού γένους, αφού τα πυθαγόρεια της οκτάβας, τετραχόρδου και πενταχόρδου είναι στάνταρ), αλλά καθαρώς
ακουστικά (=Αριστόξενος), στη συνέχεια όμως να οριστούν με λόγους μαθηματικώς (=Πυθαγόρας).
- Αν και κατηγορεί το Χρύσανθο για την ελαττωματική κλίμακά του και την ασυνέπεια λόγων και μορίων κλίμακας (και δικαίως), εν τούτοις διατήρησε τη λογική του όπως την περιέγραψα παραπάνω, ορίζοντας μη όμοιους ελάσσονα και ελάχιστο τόνο (800/729 και 27/25, δηλ. 10 και 8/72 αντίστοιχα) οι οποίοι μάλιστα, αν τους δείτε ασυγκέραστους, δεν απέχουν ομοίως, όπως φαίνεται, αλλά σχεδόν ακριβώς όπως και τα τμήματα του Χρυσάνθου, τα οποία, σε αναλογία στην κλίμακα των 72, είναι στην ουσία ίδια με αυτά της Πατριαρχικής Επιτροπής, όπως έδειξα αναλυτικά
εδώ (αφού ο ελάσσων της Πατριαρχικής είναι 9.65/72 και ο ελάσσων
των τμημάτων του Χρυσάνθου 9.53/72).
- Επεσήμανε τη διαφορά της βυζαντινής κλίμακας από τη φυσική κλίμακα του Διδύμου/Zarlino, κάτι που το έκανε και ο Χρύσανθος στο Θεωρητικό του, καθιστώντας έτσι σαφές ότι
στη βυζαντινή μουσική ο ελάσσων τόνος είναι μικρότερος από τον ελάσσονα της φυσικής κλίμακας, ο οποίος θεωρείται ευρωπαϊκής φύσεως (9.65 ο ελάσσων της Επιτροπής / 10.94 ο ελάσσων του Διδύμου) και μάλιστα συγκεκριμενοποίησε και τον τρόπο:
ο ελάσσων της φυσικής κλίμακας προκύπτει με την αφαίρεση ενός διδύμειου κόμματος (81/80) από τον μείζονα τόνο, ενώ ο ελάσσων της βυζαντινής προκύπτει με την αφαίρεση δύο διδύμειων κομμάτων.
Έτσι λοιπόν προέκυψε η κλίμακα που χρησιμοποιούμε σήμερα. Μετά τα παραπάνω, νομίζω ο καθένας είναι σε θέση να καταλάβει γιατί εξανίσταμαι
εδώ, όταν βλέπω στον 21ο μ.Χ. αι., με υπολογιστές, λογαρίθμους και δε συμμαζεύεται, οι περισσότεροι θεωρητικοί της μουσικής μας να δέχονται τα τμήματα της Επιτροπής 12-10-8, να λένε όμως ότι αυτά προέρχονται όχι από τους λόγους της Επιτροπής, αλλά από αυτούς του... Διδύμου, οι οποίοι όμως, όπως είδαμε, βγάζουν 12-11-7!!

Αν απλώς γράψετε τους λόγους στο excel που ανεβάσαμε σε προηγούμενο μήνυμα, θα δείτε το λάθος. Το γράψαμε κι αλλού, αν μας πάρει είδηση κανας σοβαρός επιστήμονας από τη γείτονα χώρα, θα μας κυνηγήσει, δεν τη γλιτώνουμε...