The correct πρώτος ήχος is the ancient Dorian with the semitone as first interval.
The 19th century theory is wrong.
Here I explain the correct mapping of now to ancient chords. Seee the diagrams
Just finished reading your article.
Very interesting information you shared, though you should later post an updated version, as your article needs more academic rigor, mainly you need a more broad bibliography, with proper footnotes after each citation, and a bibliography at the end citing every source you consulted, including the ones you didn't cite (for the style, you could choose either Chicago or APA).
I remember seeing on the Psaltologion website a screenshot of your debate with Western scholars about Ancient Greek Music from some years ago, I am definitely certain that they ignored your arguments (even though you had very good arguments and their theories are flawed in many places), precisely because of the form in which you wrote.
Let's see what I understood from your article.
- You seem to start you argumentation from the syntonic diatonic of Aristoxenos, that is 6-12-12:
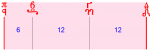
- Then expand saying that the soft diatonic would be the result of a softening of the Lichanos, giving the scale 6-9-15:

Here, I do see that you are taking Aristoxenos' intervals for granted. Still, there is the problem that these were exclusively impressions of Aristoxenos on how the tunings work, and don't necessarily reflect the reality of the actual tunings.
This is because, in order to give precise sizes for the intervals, you need to know logarithmic calculations, which Aristoxenos definitely didn't know.
Then, if I remember well, Aristoxenos said that the ear of the singer is enough to tune the instrument, and you don't need arithmetic calculations for the ratios between the frequencies, like the Pythagoreans did (CITATION NEEDED). As a result, there would be countless varieties in tuning, as each musician would tune his instruments according to his ear, and not based on precise ratios.
As a result, I would first and foremost rely on mathematical ratios between the intervals than what the ancients write about the size of those intervals.
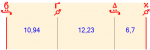
For example, Ptolemy in his first book of Harmonics says that the soft diatonic scale is 12-18-30, that is the same as 6-9-15 of Aristoxenos, but, when you actually see the ratios proposed in his book, you see that they are 21/20, 10/9, 8/7:

Which is EXTREMELY different in tuning, by all standards, because he is off tune by 2 moria for the ratio between the Parhypate and the Lichanos.
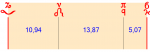
In fact, 10,94 is closer to 12 than it is to 9, meaning that all the sizes of intervals suggested by the ancients are unreliable for tuning purposes.
For this reason, when it comes to the actual tuning, I would mainly rely on Ptolemy and Al-Farabi and Chrysanthos' ratios rather than interval sizes.
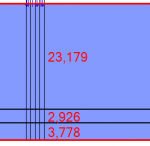
Now, if when we go to our scale here, what would we get if we try to harmonize our soft chromatic scale from Βου to Κε, so that it would be a perfect fourth (4/3)?

The end result would be the following:

Then, if you want the Γα-Δι interval to turn into a whole tone, by lowering the Δι:
Does this look to you like the diphonia of Ἦχος Δεύτερος or Ἦχος Πλάγιος τοῦ Δευτέρου? To me, it looks more like a tone-tone-semitone Major Scale tetrachord. It seems very clear to me that our Byzantine scales cannot come from the Soft Diatonic of the Ancients.
Let's go forward, to see what else we can find.
For Ἦχος Βαρύς, we get the same result as for the expected diphonia of Ἦχος Δεύτερος and Ἦχος Πλάγιος τοῦ Δευτέρου:
This does indeed look like Ἦχος Βαρύς, just note the one you expected, you instead get the one with a whole tone between Ζω and Νη, the one called Ἦχος Βαρύς Ἐνἁρμόνιος.
For Ἦχος πλάγιος τοῦ Τετάρτου, you get the Western Major Scale:

It seems pretty clear that if we want to establish the continuity between the Music of the Ancients and the music of our Church, that we should rather pursue another path, that of the equable diatonic of Ptolemy, that would evolve into Al-Farabi's scale (who likely took this scale from the Byzantines) of 9/8, 12/11, 88/81 (same scale that was used by Chrysanthos).
It gives off more consistent results, for the derivation of our scales.
By adjusting the Βου-Κε interval to a perfect fourth (4/3) through the lowering of the Κε, we actually get a real diphonia:

And what's even better, you don't need to do the extra step you did, that is lowering the Δι.
Naturally, Ἦχος Βαρύς Διατονικός uses the exact same tetrachord.
All modes can be explained by being derivations of the scale of Al-Farabi, through adjustments for the perfect fourth and perfect fifth upwards from the base.
But I do indeed agree that originally the Πα-Βου interval was smaller than the Βου-Γα, but by how much, we see that it can vary a lot, up to the point that they are almost equal in some tunings, such as Ptolemy's equable diatonic 12:11:10.
I also agree with you in that the Πα in our diatonic scale most likely represents the Hypate Meson of the Ancients.